网络层

基类

代码注解

struct layer {
    string name;
    vec_batch out, grad;
    int batch_sz;
    bool train_mode;

    layer(const string &name) : name(name), batch_sz(0), train_mode(1) {}

• name 是这层的类型和形状的信息。
• out 和 grad 保存的是每一个 batch 的输出和梯度。
• batch_sz 是当前训练时的 batch size
• train_mode 是目前的模式，初始设为训练模式

---

代码注解

    // 更改batch-size 和 trainmode 选项
    void set_train_mode(const bool &new_train_mode) { train_mode = new_train_mode; }
    virtual void _resize(int){};
    void resize(int new_batch_sz) {
        if (batch_sz != new_batch_sz) {
            batch_sz = new_batch_sz;
            out.resize(batch_sz);
            grad.resize(batch_sz);
            _resize(batch_sz);
        }
    }

然后就是一些用于更改这层网络属性的函数：

• set_train_mode 用来修改目前的模式
• resize 用来更改 batch_sz
• _resize 是一个回调函数，对于自定义的网络层，如果需要根据 batch_sz 的大小而调整某些东西，可以重写这个函数。

---

代码注解

    virtual void forward(const vec_batch &in) {}
    virtual void backward(const vec_batch &, const vec_batch &) = 0;

    virtual void clear_grad() {}
    virtual void write(ostream &io) {}
    virtual void read(istream &io) {}
    virtual void upd(optimizer &opt) {}
};

• forward 用来前向传播
• backward 用来反向传播，其中第一个参数是上一层网络的输出，第二个参数是下一层网络返回的梯度
• clear_grad 里写每次反向传播，把梯度数组清零的数组
• read 用于从一个输入流读取网络参数，write 用于把网络参数输出到一个流，注意传入的流都是二进制流
• upd 传入一个优化器，用这个优化器来优化网络参数

线性层

---

代码注解

struct linear : public layer {
    const int in_sz, out_sz;
    // 系数，系数梯度
    mat weight, grad_weight;
    vec bias, grad_bias;
    linear(int in_sz, int out_sz)
        : layer("linear " + to_string(in_sz) + " -> " + to_string(out_sz))
        , in_sz(in_sz)
        , out_sz(out_sz)
        , weight(out_sz, in_sz)
        , grad_weight(out_sz, in_sz)
        , bias(out_sz)
        , grad_bias(out_sz) {
        bias.setZero();
        for (auto &i : weight.reshaped()) i = nd(0, sqrt(2. / in_sz));
    }
    void forward(const vec_batch &in) {
        for (int i = 0; i < batch_sz; i++) out[i] = weight * in[i] + bias;
    }

• weight 和 grad_weight 分别为权值矩阵和权值矩阵的梯度。
• bias 和 bias_weight 分别为梯度向量和梯度向量的梯度。

默认采用 Kaiming He 初始化初始化系数： $$ W \sim \mathcal N(0,\sqrt {\frac 2{\text{输入向量长度}}}) $$

线性层的正向传播： $$ O=W \cdot I + B $$

---

代码注解

    void clear_grad() {
        grad_weight.setZero();
        grad_bias.setZero();
    }
    void backward(const vec_batch &in, const vec_batch &nxt_grad) {
        for (int i = 0; i < batch_sz; i++) {
            grad_bias += nxt_grad[i];
            grad_weight += nxt_grad[i] * in[i].transpose();
            grad[i] = weight.transpose() * nxt_grad[i];
        }
        grad_weight /= batch_sz;
        grad_bias /= batch_sz;
    }
    void upd(optimizer &opt) {
        opt.upd(to_vecmap(weight), to_vecmap(grad_weight));
        opt.upd(to_vecmap(bias), to_vecmap(grad_bias));
    }
    void write(ostream &io) {
        for (auto &i : weight.reshaped()) io.write((char *)&i, sizeof(i));
        for (auto &i : bias.reshaped()) io.write((char *)&i, sizeof(i));
    }
    void read(istream &io) {
        for (auto &i : weight.reshaped()) io.read((char *)&i, sizeof(i));
        for (auto &i : bias.reshaped()) io.read((char *)&i, sizeof(i));
    }
};

线性层的反向传播： $$ \begin{aligned} grad(B_i)&=grad(I_{i+1})\cr grad(W_i)&=grad(I_{i+1})\cdot I_i^T\cr grad(I_i)&=W_i^T\cdot grad(I_{i+1}) \end{aligned} $$

批归一化层

代码注解

struct batchnorm : public layer {
    // 平均值，方差
    vec mean, running_mean, grad_mean;
    vec var, running_var, grad_var, inv_var;
    vec gama, grad_gama;
    vec beta, grad_beta;
    // 这两个用来辅助,inv记录1/sqrt(方差+eps)
    vec grad_normalized_x;
    const float momentum;
    batchnorm(int sz, float momentum = 0.9)
        : layer("batchnorm " + to_string(sz))
        , mean(sz)
        , running_mean(sz)
        , grad_mean(sz)
        , var(sz)
        , running_var(sz)
        , grad_var(sz)
        , inv_var(sz)
        , gama(sz)
        , grad_gama(sz)
        , beta(sz)
        , grad_beta(sz)
        , momentum(momentum) {
        gama.setOnes();
        beta.setZero();
    }

大多数变量都可以根据名字看出意义。

特别的，gama 初始化为 1。beta 初始化为 0。批归一化层一般都这么初始化

---

代码注解

    void forward(const vec_batch &in) {
        if (train_mode) {
            mean.setZero();
            var.setZero();
            for (int i = 0; i < batch_sz; i++) mean += in[i];
            mean /= batch_sz;
            for (int i = 0; i < batch_sz; i++) var += (in[i] - mean).cwiseAbs2();
            var /= batch_sz;
            inv_var = rsqrt(var.array() + EPS);
            running_mean = running_mean * momentum + mean * (1 - momentum);
            // 使用无偏方差
            // running_var = running_var * momentum + var * batch_sz / (batch_sz - 1) * (1 - momentum);
            running_var = running_var * momentum + var * (1 - momentum);

            for (int i = 0; i < batch_sz; i++)
                out[i] = (in[i] - mean).array() * inv_var.array() * gama.array() + beta.array();
        } else {
            for (int i = 0; i < batch_sz; i++)
                out[i] =
                    (in[i] - running_mean).array() * rsqrt(running_var.array() + EPS) * gama.array() + beta.array();
        }
    }

batch norm 层前向传播（训练时实时计算方差平均值，预测时使用方差的移动平均计算）：

求方差的移动平均时，使用无偏还是有偏方差这点暂无定论，原论文是无偏，但是各种框架里似乎怎么写的都有，这里采用有偏方差。

---

代码注解

    void backward(const vec_batch &in, const vec_batch &nxt_grad) {
        for (int i = 0; i < batch_sz; i++) {
            grad_normalized_x = nxt_grad[i].array() * gama.array();

            grad_var.array() += grad_normalized_x.array() * (in[i] - mean).array();
            grad_mean.array() += grad_normalized_x.array();

            grad[i] = grad_normalized_x.array() * inv_var.array();

            grad_beta.array() += nxt_grad[i].array();
            grad_gama.array() += nxt_grad[i].array() * (in[i] - mean).array() * inv_var.array();
        }
        grad_var = -0.5 * grad_var.array() * inv_var.array().cube();
        grad_mean = -grad_mean.array() * inv_var.array();
        for (int i = 0; i < batch_sz; i++)
            grad[i].array() += (grad_mean.array() + 2 * grad_var.array() * (in[i] - mean).array()) / batch_sz;
        grad_beta /= batch_sz;
        grad_gama /= batch_sz;
    }

batch normalization 的反向传播

---

代码注解

    void clear_grad() {
        grad_gama.setZero();
        grad_beta.setZero();
        grad_mean.setZero();
        grad_var.setZero();
    }
    void upd(optimizer &opt) {
        opt.upd(to_vecmap(beta), to_vecmap(grad_beta));
        opt.upd(to_vecmap(gama), to_vecmap(grad_gama));
    }
    void write(ostream &io) {
        for (auto &i : gama.reshaped()) io.write((char *)&i, sizeof(i));
        for (auto &i : beta.reshaped()) io.write((char *)&i, sizeof(i));
        for (auto &i : running_mean.reshaped()) io.write((char *)&i, sizeof(i));
        for (auto &i : running_var.reshaped()) io.write((char *)&i, sizeof(i));
    }
    void read(istream &io) {
        for (auto &i : gama.reshaped()) io.read((char *)&i, sizeof(i));
        for (auto &i : beta.reshaped()) io.read((char *)&i, sizeof(i));
        for (auto &i : running_mean.reshaped()) io.read((char *)&i, sizeof(i));
        for (auto &i : running_var.reshaped()) io.read((char *)&i, sizeof(i));
    }
};

batch norm 层不仅需要保存权值，还需要保存算出来的移动平均

卷积层

---

代码注解

ten3 hi_dim_conv(const ten3 &input, const ten4 &kernel, ten3 &res) {
    int sz1 = input.dimension(1) - kernel.dimension(2) + 1;
    int sz2 = input.dimension(2) - kernel.dimension(3) + 1;
    res = ten3(kernel.dimension(1), sz1, sz2);
    res.setZero();
    for (int i = 0; i < kernel.dimension(0); i++)
        for (int j = 0; j < kernel.dimension(1); j++)
            res.chip(j, 0) += input.chip(i, 0).convolve(kernel.chip(i, 0).chip(j, 0), Eigen::array<int, 2>{0, 1});
    return res;
}

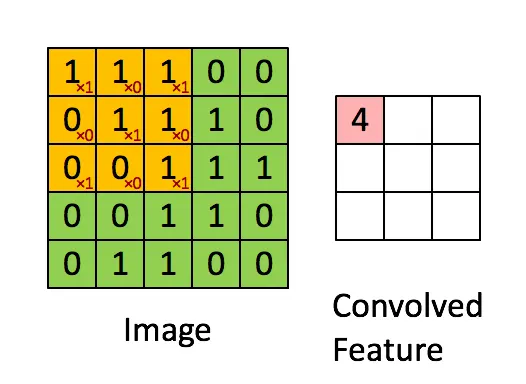
这里用 Eigen 自带的二维卷积写了一个 3 维度卷积的函数。

---

代码注解

struct conv : public layer {
    const int in_channel, out_channel, in_rows, in_cols;
    const int out_rows, out_cols;
    const int k_rows, k_cols;
    ten4 kernel, grad_kernel;
    vec bias, grad_bias;
    conv(int in_channel, int out_channel, int in_rows, int in_cols, int k_rows, int k_cols)
        : layer("conv " + to_string(in_channel) + " channels * " + to_string(in_rows) + " * " + to_string(in_cols) +
                " -> " + to_string(out_channel) + " channels * " + to_string(in_rows - k_rows + 1) + " * " +
                to_string(in_cols - k_cols + 1))
        , in_channel(in_channel)
        , out_channel(out_channel)
        , in_rows(in_rows)
        , in_cols(in_cols)
        , out_rows(in_rows - k_rows + 1)
        , out_cols(in_cols - k_cols + 1)
        , k_rows(k_rows)
        , k_cols(k_cols)
        , kernel(in_channel, out_channel, k_rows, k_cols)
        , grad_kernel(in_channel, out_channel, k_rows, k_cols)
        , bias(out_channel)
        , grad_bias(out_channel) {
        bias.setZero();
        for (int i = 0; i < in_channel; i++)
            for (int j = 0; j < out_channel; j++)
                for (int k = 0; k < k_rows; k++)
                    for (int l = 0; l < k_cols; l++)
                        kernel(i, j, k, l) = nd(0, sqrt(2. / (in_channel * in_rows * in_cols)));
    }

依然是 He 初始化，这里 fan_in 即与每个权值相乘的输入的个数应该是 in_channel * in_rows * in_cols。

---

代码注解

    void forward(const vec_batch &in) {
        for (int i = 0; i < batch_sz; i++) {
            vec tmp_vec = in[i];
            ten3 tensorout;
            hi_dim_conv(ten3map(tmp_vec.data(), in_channel, in_rows, in_cols), kernel, tensorout);
            for (int j = 0; j < out_channel; j++) tensorout.chip(j, 0) = tensorout.chip(j, 0) + bias[j];
            out[i] = to_vecmap(tensorout);
        }
    }

这里进行的是完全卷积，卷积层前向传播： $$ O=I\otimes W+B $$

---

代码注解

    void clear_grad() {
        grad_bias.setZero();
        grad_kernel.setZero();
    }
    void backward(const vec_batch &in, const vec_batch &nxt_grad) {
        for (int i = 0; i < batch_sz; i++) {
            vec _nxt_grad = nxt_grad[i], _in = in[i];
            grad[i].resize(in[0].size());
            ten3map grad_out(_nxt_grad.data(), out_channel, out_rows, out_cols);
            ten3map grad_in(grad[i].data(), in_channel, in_rows, in_cols);
            ten3map in_map(_in.data(), in_channel, in_rows, in_cols);
            grad_in.setZero();
            for (int j = 0; j < out_channel; j++) {
                grad_bias(j) += ten0(grad_out.chip(j, 0).sum())();
                for (int k = 0; k < in_channel; k++) {
                    // 转180°的卷积核
                    ten2 rot_kernel = kernel.chip(k, 0).chip(j, 0).reverse(Eigen::array<bool, 2>{true, true});
                    ten2 in_ten = grad_out.chip(j, 0).pad(Eigen::array<pair<int, int>, 2>{
                        pair<int, int>{k_rows - 1, k_rows - 1}, pair<int, int>{k_cols - 1, k_cols - 1}});
                    grad_in.chip(k, 0) += in_ten.convolve(rot_kernel, Eigen::array<int, 2>{0, 1});
                    // (i,j)--(k,l)-->(i-k,j-l)
                    grad_kernel.chip(k, 0).chip(j, 0) +=
                        in_map.chip(k, 0).convolve(grad_out.chip(j, 0), Eigen::array<int, 2>{0, 1});
                }
            }
        }
        grad_bias /= batch_sz;
        grad_kernel = grad_kernel / (float)batch_sz;
    }

卷积层的反向传播，较为复杂。 参考这个网站

激活函数层

这里以 sigmoid 为例：

---

代码注解

struct sigmoid : public layer {
    sigmoid() : layer("sigmoid") {}
    void forward(const vec_batch &in) {
        for (int i = 0; i < batch_sz; i++)
            out[i] = in[i].unaryExpr([](float x) -> float { return 1. / (exp(-x) + 1); });
    }
    void backward(const vec_batch &in, const vec_batch &nxt_grad) {
        for (int i = 0; i < batch_sz; i++)
            grad[i] = nxt_grad[i].cwiseProduct(out[i].unaryExpr([](float x) -> float { return x * (1. - x); }));
    }
};

sigmoid 层前向传播 $$ O=\frac 1{e^{-I}+1} $$ 反向传播( 表示逐位相乘) $$ grad(I_i)=grad(I_{i+1})I_i*(1-I_i) $$